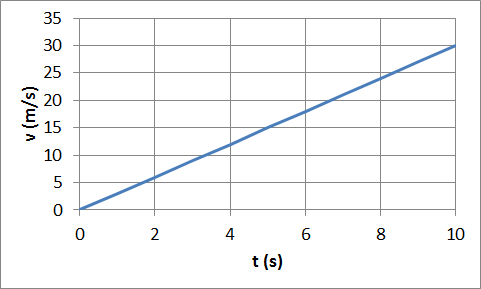
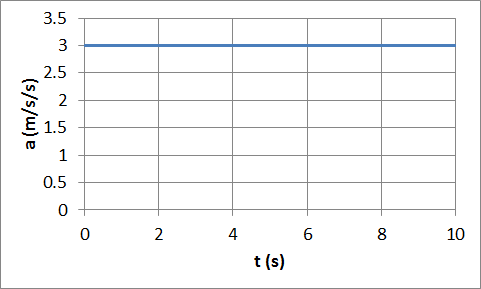
Let us assume at t = 0 a cart is leaving the origin with zero initial velocity and constant acceleration of 3 m/s² in the positive x-direction. 
Then a = ∆v/∆t,  v_f - v_i = a(t_f - t_i), and since v_i = t_i = 0 we have v(t) = a*t = (3 m/s²)*t.
The velocity (m/s) versus time (s) graph is a straight line with a slope of 3.
The acceleration (m/s²) versus time (s) graph yields a straight line (a = 3) with zero slope.

 

Kinematic equations for one-dimensional motion with constant acceleration

Let us consider one-dimensional motion in the x-direction.
Let us make this explicit by using the subscript x. 
The average acceleration equals the instantaneous acceleration.  From

a_x = (v_xf - v_xi)/(t_f - t_i)

we obtain

a_x(t_f - t_i) = (v_xf - v_xi),

or

v_xf = v_xi + a_x∆t.

The velocity versus time graph is a straight line. 
The average velocity in a time interval ∆t therefore is just the sum of the final and the initial velocities divided by 2,

v_x(avg) = (v_xf + v_xi)/2.

The displacement is ∆x = v_x(avg)∆t.  We can rewrite this expression to obtain x_f - x_i = ½(v_xf + v_xi)∆t, or

x_f - x_i = v_xi∆t + ½a_x∆t².

We can also express the velocity as a function of the displacement.
∆x = ½(v_xf + v_xi)∆t = ½ (v_xf + v_xi)(v_xf - v_xi)/a_x = (v_xf² - v_xi²)/(2a_x) yields

v_xf² = v_xi² + 2a_x(x_f - x_i).

The equations in red are the kinematic equations for motion in the x-direction with constant acceleration.

AI Study Tip:

Ask an AI to help you develop a strategy to pick the right tool (equation) for a problem.
Example prompt:  'I am about to solve a constant acceleration problem.  I am given initial velocity v_i, displacement ∆x, and time ∆t, but I don't know the final velocity v_f or acceleration a.  Walk me through the logic of which kinematic equation I should use first and why.  Don't solve it for me.  Just help me pick the right "tool" from the toolkit.'

What does a position versus time graph look like for motion in one dimension with constant acceleration?

Choose your coordinates so that x_i = t_i = 0.  Then x = v_it + ½at². 
This is the equation of a parabola.  The position versus time graph is a section of a parabola. 
In the limit a = 0 it becomes a straight line.

Examples:

Problem:

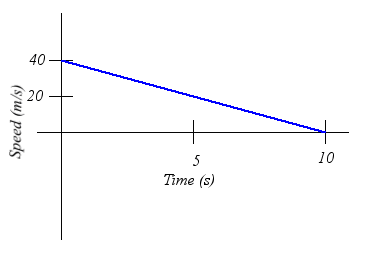The speed versus time graph on the right represents the motion of a car.  Approximately how far did the car travel during the first 5 seconds?

Solution:

• Reasoning:
  The speed versus time graph is a straight line.  We have motion with constant acceleration.  The slope of the graph represents the acceleration.
• Details of the calculation:
  The slope of the graph represents the acceleration.
  a_x = (v_xf - v_xi)/(t_f - t_i) = (-40 m/s)/(10 s ) = -4 m/s².
  For motion with constant acceleration we have
  ∆x_i = v_xi∆t + ½a_x∆t².
  After 5 s we have
  ∆x = 40m/s * 5 s - ½(4 m/s²)*(5 s)² = 150 m.
  During the first 5 seconds the car traveled 150 m.

Problem:

Blood is accelerated from rest to v = 30.0 cm/s in a distance of 1.80 cm by the left ventricle of the heart.  Assume constant acceleration. 
(a)  Find the acceleration a.
(b)  For how long does the blood accelerate?
(c)  Is the answer reasonable when compared with the time for a heartbeat?

Solution:

• Reasoning:
  We assume motion with constant acceleration in one dimension.  The kinematic equations for this type of motion are
  v_xf = v_xi + a_x∆t,  x_f - x_i = v_xi∆t + ½a_x∆t²,  and v_xf² = v_xi² + 2a_x(x_f - x_i).
• Details of the calculation:
  (a)  Given:  v_i = 0, v_f = 0.3 m/s, ∆v = 0.3 m/s.
  x_i = 0, x_f = 0.018m, ∆x = 0.018 m.
  Kinematic equation:  v_xf² = v_xi² + 2a_x(x_f - x_i).
  Solve for a_x = (v_xf² -  v_xi²)/(2(x_f - x_i)) = (0.3 m/s)²/(0.036 m) = 2.5 m/s².
  
  (b)  v = at, t = v/a = (0.3 m/s)/(2.5 m/s) = 0.12 s
  or v_x(avg) = (v_xf + v_xi)/2 = 0.15 m/s.  ∆x = v_x(avg)∆t, 
  ∆t = ∆x/v_x(avg) = 0.018 m/(0.15 m/s) = 0.12 s.
  
  (c)  The figure below shows a typical electrocardiogram waveform.  0.12 s seems a reasonable acceleration time.
  

Free Fall

Systematic experiments on freely falling objects were carried out by Galileo Galilei (1564-1642).  Near the surface of the earth all freely falling objects accelerate at approximately the same rate.  This acceleration is denoted by g.  Its direction is downwards, towards the center of the earth.  Freely falling objects move with constant acceleration g = 9.8 m/s² downward.

Problem:

You drop a ball from a window on an upper floor of a building.  It strikes the ground with speed v.  You now repeat the drop, but you have a friend down on the street, who throws another ball upward with the same speed v.  Your friend throws the ball upward at the same time you drop yours from the window.  At some location the balls pass each other.  Is this location at the halfway point between the window and the ground, above this point, or below this point?

Solution:

• Reasoning:
  Both balls are accelerating.  The ball thrown upward will reach the window at the same time the dropped ball reaches the ground.  The speed of the dropped ball increases linearly with time.  The ball moves with the slowest speed near the window and with the fastest speed near the point it hits the ground.  In half the time it takes to reach the ground it covers less than half the distance and is still above the midpoint between window and ground.  The speed of the ball thrown upwards decreases linearly with time.  It moves fastest near the ground and slowest near the window.  In half the time it takes to reach the window, it is already above the midway point.  The two balls therefore meet above the midway point.
  
  We can also work with our kinematic equations.
  Assume the ball falls for 1 second.  The speed of the falling ball as a function of time is v = 9.8 (m/s²) t and the distance traveled is d = ½ 9.8 (m/s²) t².  In one second the ball travels 4.9 m.  The velocity of the falling ball as a function of time is v = -9.8 (m/s²) t j and its position as a function of time is r = (4.9 m - ½ 9.8 (m/s²) t²) j.
  The velocity of the rising ball as a function of time is v = (9.8 (m/s) - 9.8 (m/s²) t) j and its position as a function of time is r = (9.8 (m/s) t - ½ 9.8( m/s²) t²) j.  Graphs of velocity and position vs. time for the two balls are shown below.

 

Problem:

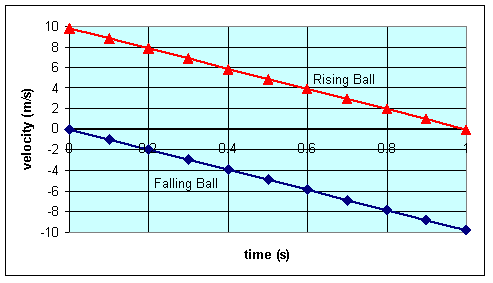
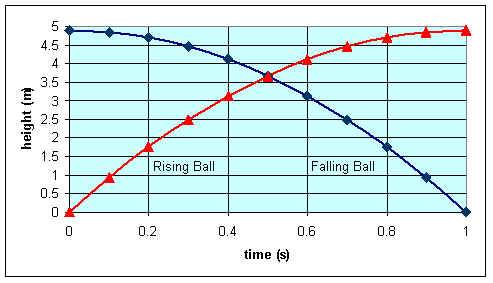
A stone is thrown directly upward with an initial speed of 4 m/s from a height of 20 m.  After what time interval does the stone strike the ground?

Solution:

• Reasoning:
  We have motion in one dimension with constant acceleration.  Put the origin of your coordinate system at the position of the stone at t = 0 and let the x-axis point straight downward.  Then we know that
  x_i = 0, v_xi = -4 m/s, t_i = 0,
  x_f = 20 m, v_xf = ?, t_f = ?,
  a_x = 9.8 m/s².
  We are asked to solve for t = t_f.
• Details of the calculation:
  We have x_f - x_i = v_xi∆t + ½a_x∆t², 20 m = -4 (m/s) t + 4.9 (m/s²) t².
  We rewrite this equation as t² - (4 s/4.9) t - (20 s²/4.9) = 0, or t² - (0.816 s)t - 4.08 s² = 0.
  This is a quadratic equation with two solutions.
  t = (0.816 s)/2 ± sqrt[((0.816 s)/2)² + 4.08) = 0.408 s ± 2.061 s
  Only the + sign makes sense.  We find t = 2.47 s

Problem:

What is the speed of the stone in the previous problem when it hits the ground?

Solution:

• Reasoning:
  There are different ways to find the answer.  One way is to use the equation v_xf² = v_xi² + 2a_x(x_f - x_i).
  All the quantities on the right-hand side are known, we can solve for v_xf.
• Details of the calculation:
  Here (x_f - x_i) = 20 m, a_x = 9.8 m/s², and v_xi = -4m/s.
  Therefore v_xf² = (16 + 2*9.8*20)(m/s)², v_xf = 20.2 m/s.

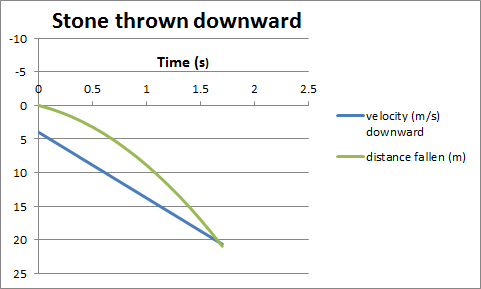
Note:  If the stone is thrown directly downward with an initial speed of 4 m/s, it hits the ground with the same speed, but at an earlier time.

 

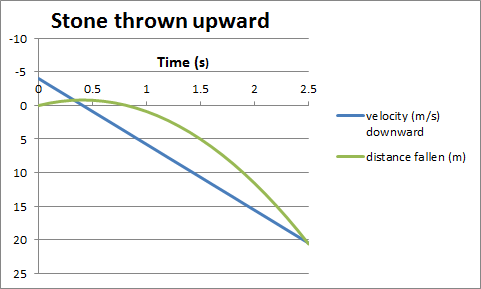
When the stone thrown upward returns to its original position, its velocity is -v_i. 
The magnitude is that of the initial velocity, but the sign of the velocity has changed.
The velocity is now in the downward direction.
From then on, the stone behaves exactly like a stone throw downward with the same initial speed.

AI Study Tip:

Ask an AI to give you some short word problems.
Example prompt:  'Give me a short word problem about the acceleration of a Cheetah leaping from rest to its top speed, or a frog jumping.  Ask me to calculate the acceleration and the distance covered.  Once I provide my answer, check my units (m/s²) and my significant figures.'